The framework of modern physics largely rests on two pillars, namely General Relativity (which is celebrating its centenary this year), and Quantum Mechanics. Albert Einstein not only formulated the theory of relativity but was also one of the pioneers in the development of Quantum Theory. However, it is worth noting that Einstein had his reservations about the inherent ‘weirdness’ and unpredictability that prevails in Quantum Mechanics and famously said, ‘’God does not play dice’’. Despite facing criticism from physicists and philosophers alike, Quantum Mechanics has stood the test of time and every experiment that have been performed so far has been found to be consistent with Quantum Mechanics.

In this particular article, I’m going to attempt to simplify the ‘spooky’ phenomenon called quantum entanglement, which gave birth to the EPR paradox. The results are counter-intuitive, and have troubled even the most accomplished physicists for decades. 

Understanding Quantum Entanglement

Before delving into Quantum entanglement, it is essential to understand a few key concepts of quantum mechanics which are remarkably different from the world described by classical mechanics. In classical mechanics, the state of a particle can be described completely by its position and momentum. We however know that the Uncertainty principle restricts us to measure both these quantities up to arbitrary precision and even puts an exact limit to the accuracy we can achieve.  

As an analogue, in quantum mechanics a system is described by its quantum state, which contains the probabilities of possible positions and momenta. The quantum state is described by a wave function which gives us some information about the particle. All such possible states of the system form an abstract vector space known as the Hilbert Space. The Hilbert Space is essentially a mathematical concept which extends the usage of vector algebra and calculus to a ‘n’ dimensional space, where n can be finite or infinite. In quantum mechanics, particles can have parameters that take on two (or more) values at the same time (be in two places, have two energies, have two spins, etc.). Physically, the quantum mechanical wave function which describes the particle is a superposition of several Eigen states – where Eigen states simply mean possible outcomes of any game of chance (e.g. Tossing of a coin has two possibilities i.e. head or tail).

Many people are familiar with the famous Schrödinger’s cat experiment where the cat is simultaneously dead and alive (a superposition of dead and alive states) before the box is open. Next, we need to understand the significance of measurement in quantum mechanics. Whenever we measure or observe a certain quantity, the wave function which was initially a superposition of several Eigen states appears to reduce to a single Eigen state by ”observation”. This is known as a collapse of wave function and is a key to understanding entanglement.

To be able to understand and visualise entanglement, I will present a very simple thought experiment. Consider two orange balls are packed in boxes and handed over to two brothers, John and Smith. I have used the colour orange, since the balls which are either red or yellow are in a superposed or mixed state before the box is opened. When Ram opens the box, he has equal probability of finding a red or yellow ball. Suppose he finds the ball to be red, he can predict with certainty that Shyam’s ball is yellow. We then say that the two balls are ‘entangled’. In some sense, this could be called transmitting information faster than the speed of light.  But, there is a (big) catch: we have no way of controlling which outcome the measured object will choose (here, red or yellow colour of the ball). In this sense, you could say that entanglement allows you to transmit random information faster than light. This is perhaps not useful.  We can now define Quantum Entanglement as quantum mechanical phenomenon whereby a group or pair of particles interact with each other, although they maybe at infinite separation. This results in a quantum state to be assigned to the group as a whole, rather than to the independent composite particles. Physical properties like position, momentum and spin of these particles are found to have correlated values. 

The best way to understand this, is to accept that particles can ‘exist in multiple states’ at the same time. This can seem very incompatible with our view of reality. But this is the fundamental truth of the quantum world. There is no definite value to properties until they are ‘observed’.

The physical behaviour of entanglement is very bizarre and quite difficult to comprehend. To explain the physical significance, a famous example is cited below along with an illustration.  Imagine a source that is surrounded by two brothers John and Smith. The source emits an electron-positron pair, where the electron goes to Ram and the positron goes to Shyam. According to quantum mechanics, we can arrange our source so that each emitted pair occupies a quantum state called a spin singlet. The particles are thus said to be entangled. This can be viewed as a quantum superposition of two states, which we call state I and state II. In state I, the electron has spin pointing upward along the x-axis (+x) and the positron has spin pointing downward along the x-axis (−x). In state II, the electron has spin −x and the positron has spin +x. Now, suppose John and Smith wish to measure the spins of the electron and positron respectively. Before measuring, it is impossible to predict the spins(both have 50% chance of occurring) and as stated before, the particles have both +x and -x spins.

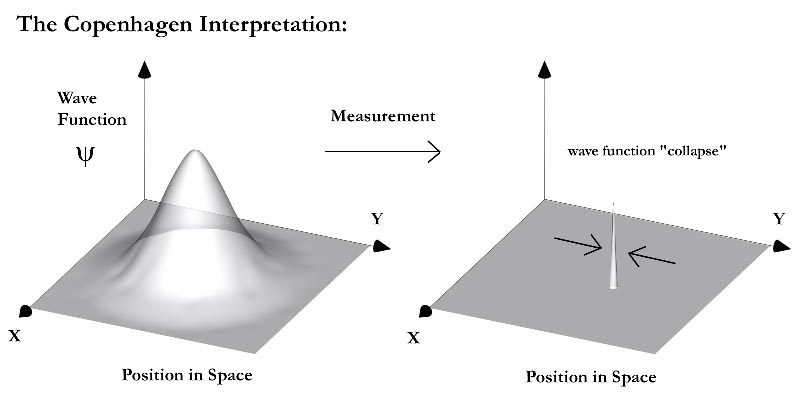
Suppose John measures the spin as +x. According to the Copenhagen interpretation of quantum mechanics, the quantum state of the system collapses into state I due to the measurement being made. The quantum state determines the probable outcomes of any measurement performed on the system. Now if Smith measures the spin along x axis of the positron, there is a 100% probability of getting -x. In quantum mechanics, the x-spin and y-spin are “incompatible observables”, meaning the Heisenberg uncertainty principle applies to alternating measurements of them: a quantum state cannot possess a definite value for both of these variables. Suppose John measures the x-spin and obtains +x, so that the quantum state collapses into state I. Now, instead of measuring the x-spin as well, Smith measures the y-spin. According to quantum mechanics, when the system is in state I, Smith y-spin measurement will have a 50% probability of producing +y and a 50% probability of –y. It is impossible to predict which outcome will appear until Shyam actually performs the measurement.

The EPR Paradox

We can extend the above argument to the more familiar properties of position and momentum as well. Thus, measuring the position of one particle, is giving rise to indeterminacy in the momentum of the other particle. This is indeed very perplexing as it implies that the second particle somehow ‘‘knows’’ the result of the measurement of position of the first particle. Einstein, Podolsky and Rosen asked how can the second particle “know” to have precisely defined position but uncertain momentum? This implies that the two particles are communicating instantaneously across space, which clearly violates the Special Theory of Relativity. This apparent discrepancy is known as the EPR paradox.

Einstein, Podolsky and Rosen presented their ideas and a way to resolve the paradox in a paper where they claimed quantum mechanics is incomplete if certain information about any state is not given; it means entanglement seems non local (even acting correlated though they are a distance apart) because the wave function was falling short of information about states. This statement directly implies about the existence of hidden variables, i.e. variables that are not known are acting here and restricting scientists to know fully about states of the system. These variables can be thought to represent the results of the measurements which are then already known to the particle being measured. However the assumption was proved wrong by von Neumann in his theorem of impossibility, where he showed that the existence of hidden variables is impossible (Rosinger, 2004, p. 1). Finally, Bell was able to disprove the presence of hidden variables mathematically. In its simplest form, the theorem states that ‘No physical theory of local hidden variables can ever reproduce all of the predictions of quantum mechanics’.

Although John Bell gave a rigorous proof against hidden variables, his paper was mostly based on mathematics and physical significance of his calculation was not clear. To prove his calculations Clauser, Horne, Shimony, and Holt (1969) published an article proposing an experiment better known as CSHS experiment which was written down as “Proposed Experiment to Test Local Hidden-Variable Theories,” in which they derived a more general form of Bell’s inequality for practical reason. Again, this experiment reinforced the notion of entanglement between the pairs of electrons.  After these experiments, many other experiments have been performed that have favoured quantum mechanics. In 2008, Salart, Baas, van Houwelingen, Gisin, and Zbinder (2008) published their Bell’s test experiment where the inequalities are still violated with pairs of particles 18 Km apart.

 

The current understanding of the EPR paradox is that the formulation of Quantum Theory is such that the effect of measurement happens instantaneously, but this cannot be used to transfer classical information. Hence, it does not violate Special Relativity. Quantum entanglement is an extremely active area of research and entanglement has been observed in photons, electrons and even large molecules. There is immense scope in the future where entanglement can possibly revolutionize communication and computation across the universe!